Color & Image Encoding

24 Sep 2018 in CS 101

How does a computer understand digital images?

Binary is the only ‘language’ computers speak. Therefore, if we want to represent numbers, letters, words, text, and images, we must first convert it into binary (0 and 1).

To store an image on a computer, the image is broken down into tiny picture elements called pixels. An image with a resolution of 11 by 7 pixels has 11 times 7 or 77 pixels. An image composed of just 77 pixels is shown below. Resolution can also refer to the density of the pixels in the display, where the unit of measurement is pixels per inch (PPI). Given a screen of 250 pixels across 5 inches, the density of pixels is 250 / 5 which is 50 PPI.

The concept of a pixel is similar to a dot in the art form pointillism. The only difference is, however, pixels fit neatly in a grid.

Monochrome (Two-Color) Images

How can we encode pixels as bits (aka binary digits)? The simplest scenario is when we’re given an image in just black and white. Another way of thinking of a black and white digital image is a grid of pixels that are either on or off. Then, we can represent each pixel as exactly one bit (either 1 = on = black or 0 = off = white).

Exercise 1

We can extend this to grids of more pixels. Below are a few examples on how we can convert 8 x 8 digital images into binary.

Exercise 2

Exercise 3

Can you do this in reverse? Instead of determining the bits from the digital image, can you determine/draw the image if given the bits? Draw the image that corresponds to each of the following hexadecimal numbers.

For example, if given the string of hexadecimal digits 3C66703C0E663C00, you can translate each group of 4 pixels into 1 hex digit.

Decode the image from these hexadecimal numbers:

• 0066ACD8366ACC00
• 7E607C0606663C00
• C6CCD8F0D8CCC600

Exercise 4

Write a 5-letter word in a 8 x 8 pixelated font. For example:

Then, translate each letter into binary, and then into hexadecimal.

In class, you will challenge your partner to decode the hexadecimal digits to read the word. Come prepared with your hex digits and grid paper.

Color

Before we start exploring how we can combine multiple colors in the same image, let’s first explore what color is.

Color refers to the wavelength of light. Light of short wave lengths are perceived as violet (a kind of bluish-purple), and the long wavelengths are perceived as red. In between these is the usual spectrum of colors: oranges, yellows, greens, blues, and purples.

As shown, color (aka visible light) is a very small section of the electromagnetic spectrum. However, there are other wavelengths that we can’t perceive at all.

From a biological stance, the anatomy of our eyes leads to another explanation of how we see color. Your retina contains detail-sensitive neurons called rods (r for resolution) and color-sensitive neurons called cones (c for color). The rods are generally color-blind, whereas the cones come in three flavors: Long-wavelength (red), Medium-wavelength (green), and Short-wavelength (blue).

Mixing colors of light (an additive model) is different from mixing colors of paint (a subtractive model).

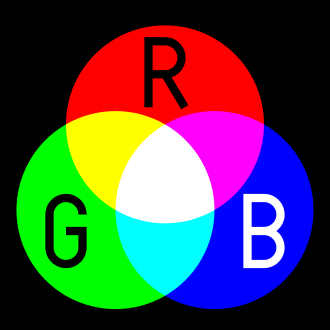
You can try mixing the primary colors of light (R = red, G = green, B = blue) using Prof. League’s RGB demo: https://contrapunctus.net/rgb-demo/4bit.html

Color Encoding

With the idea of mixing red, green, and blue to make any color, it is clear that we need more bits to represent how much of each. When we were converting monochrome (black and white) images into binary, we only needed 1 bit. With 2 bits, we can represent four numbers (0, 1, 2, and 3) and, therefore, four colors. With 3 bits, we can represent the numbers 0 to 7 (8 numbers, 8 colors).

Let’s use 3 bits, where one bit represents red, another bit represents green, and the last bit represents blue.

• 0 = 000 = red + green + blue = black
• 1 = 001 = red + green + blue = blue
• 2 = 010 = red + green + blue = green
• 3 = 011 = red + green + blue = cyan
• 4 = 100 = red + green + blue = red
• 5 = 101 = red + green + blue = magenta
• 6 = 110 = red + green + blue = yellow
• 7 = 111 = red + green + blue = white

From black and white images, we can now represent six more colors. However, to make realistic (true-color) digital images, we need a lot more color options. To have more colors, we need more bits.

Today, we typically use 24 bits to represent color. The intensity of red uses 8 bits, green’s intensity uses 8 bits, and blue’s intensity uses 8 bits. This makes a total of 24 bits.

Because each primary color gets 8 bits, it can also be represented as 2 hexadecimal digits.

You see how the hexadecimal true colors change by adjusting slider in Prof. League’s 24-bit color demo: https://contrapunctus.net/rgb-demo/index.html

To practice visualizing colors when given only the hexadecimal number, play the color guessing game What the Hex.